Why’s the Year 11 Chemistry Syllabus important?
The Year 11 Chemistry syllabus is your key to success over the next year. The syllabus lays out everything you need to know, they can’t ask you questions about anything else, so leverage it to your advantage!
The Year 11 Chemistry syllabus is split into 4 modules, which are further divided into enquiry questions. These help you group your understanding, placing similar topics together and creating a sense of ‘flow’ from one idea to another. By the end of the year, you should have an idea of what is required for each enquiry question and be able to make connections between similar enquiry questions.
How do I use a Syllabus?
Your syllabus should become your guiding light over the next few months. Eventually, when you see a year 11 chemistry question you should be able to make a connection between that question and where in the syllabus they’ve pulled it from - this will help you to include all relevant details and pick up every possible mark. You may like to consider organising your notes by syllabus dot point, summarising the relevant content under each point as you learn. This lets you be sure that you know everything that you need to (when all of the dot points have been filled out) and places you in an amazing position where you’re comfortable with what information is required for questions about each point.
‘Module 2 - Introduction to Quantitative Chemistry’ is a little different to the other modules you’ll explore in year 11, since it focuses on building the tools you need to do calculations in Chemistry, rather than lots of specific content. To be successful, you need to practice - answer as many questions as possible, get super comfortable converting between moles and other units and fully understand how limiting reagent, concentration, dilution and gas calculations work!
Key Concepts and Skills in Module 2 Introduction to Quantitative Chemistry
Module Two, also known as “Introduction to Quantitative Chemistry” introduces you to the tools to start quantifying the chemical reactions you’ve explored so far. Quantitative chemistry uses numbers to describe observations, so instead of saying “there was gas produced”, we can say “the reaction produced 2.3 L of gas”. Quantitative values give specificity to our descriptions, and are critical for industry and research alike.
How would a production line function if they didn’t know much product they could produce each day and therefore how much profit they could make?
How could Betty Crocker guarantee that their cakes would rise if a scientist couldn’t first determine how much gas is produced under different conditions?
How could we combat our changing climate without being able to quantify our observations of the changes to gas composition and temperature?
The calculations taught in module 2 are essential for specificity, efficiency and profitability, forming the basis of all calculations you’ll need through your scientific career (be that just for the HSC or beyond).
Chemical Reactions and Stoichiometry
Chemical reactions are actually physical things that happen.
This may seem like a pretty obvious statement, but is very easy to forget when you’ve been looking at long chemical equations for a while. If you ever get stuck, try to picture the molecules interacting with each other - this will help you figure out the stoichiometry and bonding that occurs in the reaction.
Stoichiometry and Balanced Chemical equations go hand-in-hand.
Stoichiometry describes the ratio that molecules in a reaction will react in, we derive this ratio from the balanced chemical equation.
The idea of a balanced chemical equation comes from the conservation of matter - the idea that nothing can be created or destroyed, only transferred or transformed from one form to another. Think back to chemical reactions as physical things actually happening, can a product just appear if none of its components were present in the reactants? Nope!
This means that when we look at a chemical reaction we must have the same number of each chemical element on both the product and reactant side. Let’s think about building a smore:
A good smore requires 2 biscuits, 1 marshmallow and 1 piece of chocolate:
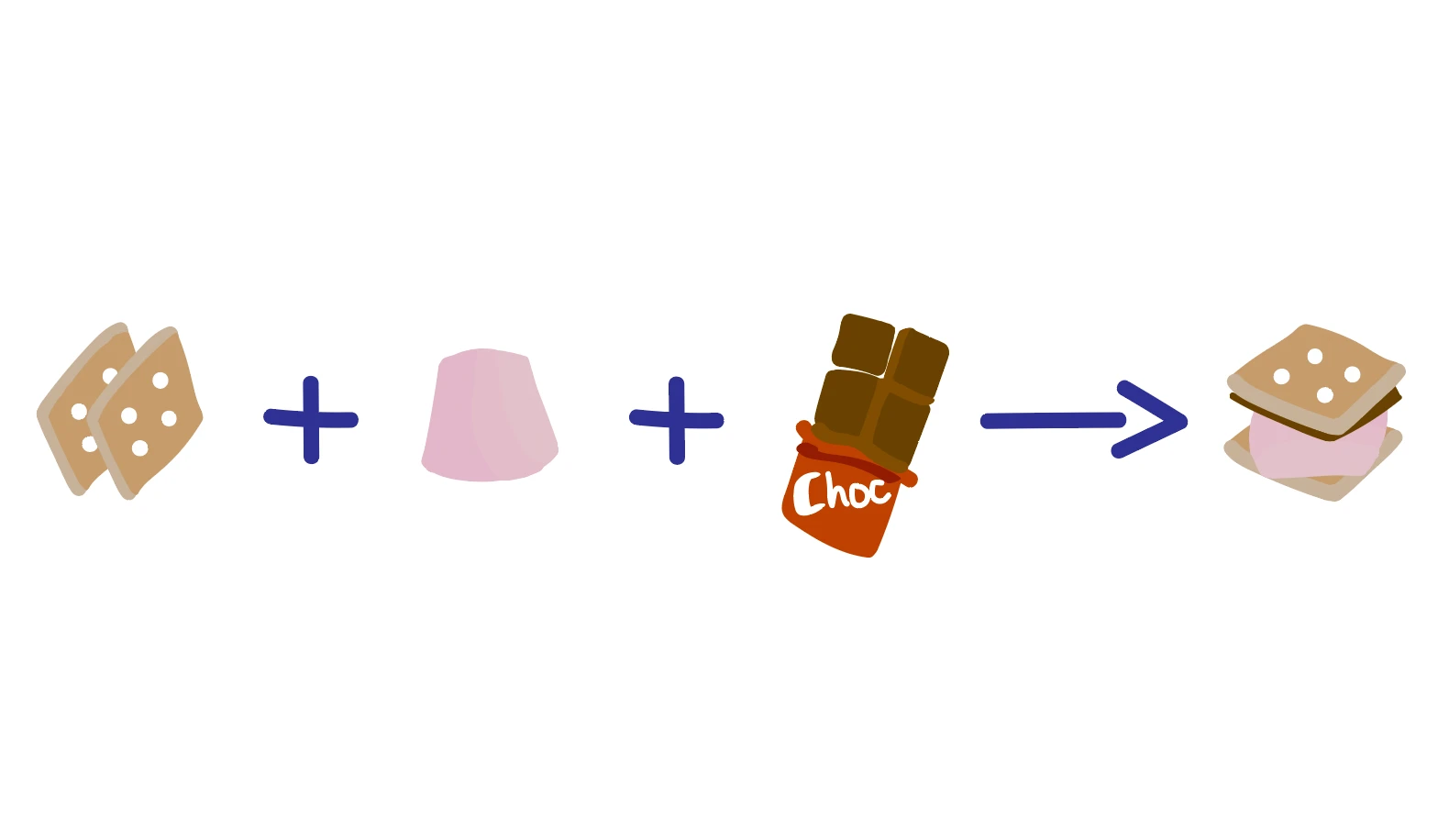
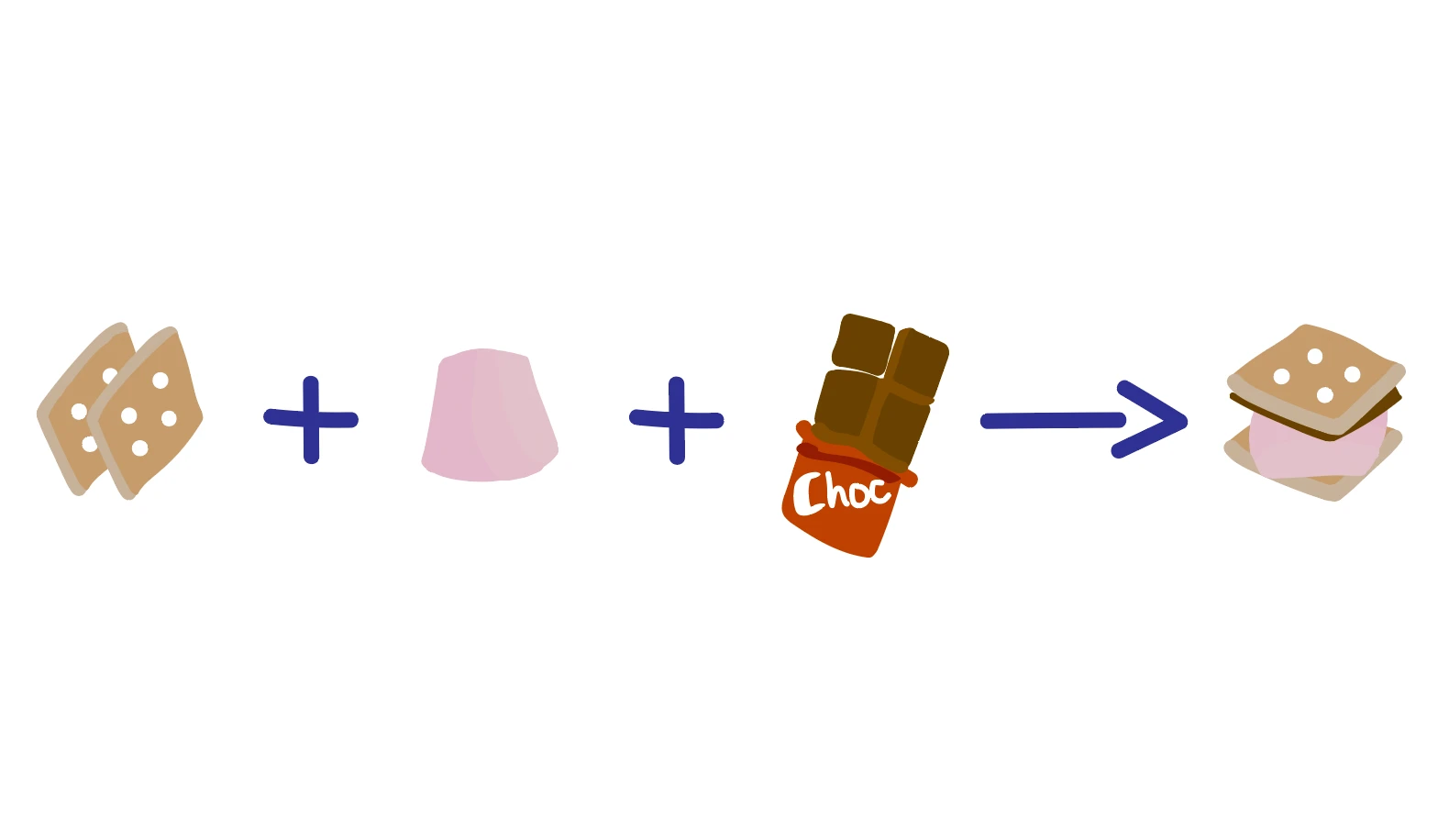
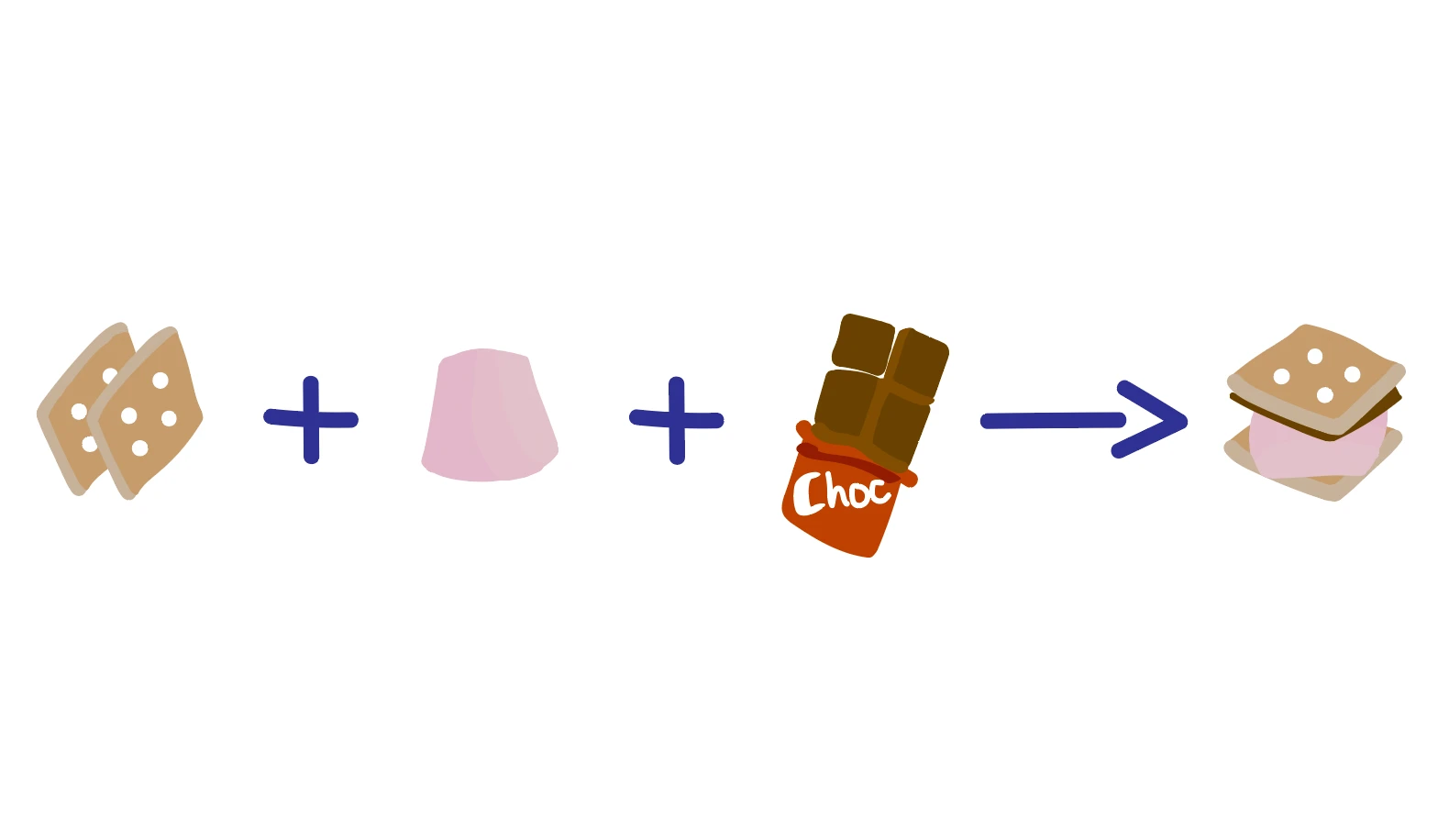
2 Biscuits + 1 Marshmallow + 1 Chocolate → 1 Smore
Notice that the biscuits, marshmallow and chocolate that are present on the reactants side are also present within the smore on the products side. No new ingredients have appeared, and none of the ingredients I started with have disappeared, therefore this is a balanced “chemical” equation!
Since we need 2 biscuits, 1 marshmallow and 1 chocolate to build 1 smore, my stoichiometric ratio is 2:1:1:1 - every time I build a smore I need that same ratio of reagents, otherwise I won’t get a complete smore!
This brings us to the very first type of calculation we can do, moles based calculations:
If I have 1 smore, how many biscuits did I start with?
Well, the ratio of smores:biscuits is 1:2, therefore I must’ve started with 2 biscuits!
If I have 5 smores, how many marshmallows did I start with?
The ratio of smores:marshmallows is 1:1, therefore I must’ve started with 5 marshmallows.
The ratio of reagents remains constant, regardless of how many extras I might add, for example:
If I have 4 biscuits, 2 marshmallows and 1 chocolate, how many smores can I make?
You might think I can make 2 smores, since I have enough biscuits and marshmallows for 2, *but* what’s a smore without the chocolate? Since, we don’t have enough chocolate to complete the 2nd smore, we can only build one.
In this case, the chocolate is the limiting reagent, it determines how much product we can make since we run out of it first. I could have 50 biscuits, but with only one piece of chocolate I can still only produce 1 smore.
The limiting reagent is the reagent that runs out first, and it determines how much of the product we can form.
Check out Q4 for more practice with stoichiometry and limiting reagents!
To balance a chemical equation we consider the number of any element on each side of the arrow, then add coefficients until there are equal amounts on both sides.
There are four easy steps to make sure that a chemical equation is balanced, with practice these should become second nature, so that you double-check that a chemical equation is balanced every single time you see one!
Stoichiometry Question Example
We’re going to work through the example of the complete combustion of Methane (CH4).
The unbalanced equation is:
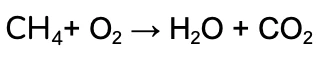
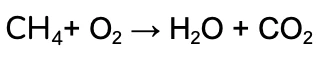
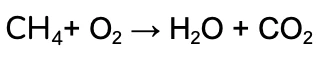
- Identify the elements in the Reactants and Products in the reaction (remember that all of the same elements should be present on both sides, in accordance with the conservation of matter!)
It may be helpful to use a table to keep track of each of the elements in the reaction, especially as you practice :).



It’s easy to see now that the equation isn’t balanced - we’ve lost two hydrogen and gained an oxygen between the reactants and the products!
- Balance one of the elements
To ‘balance’ the elements, we add a coefficient to the chemical compounds, this means we multiply every element of the compound by the coefficient.
We’re going to balance the hydrogen first, by adding a coefficient of 2 in front of the water.
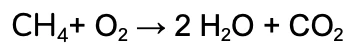
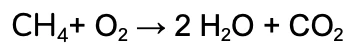
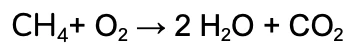



Notice that the number of oxygen on the products side also changed, since it is a part of the water compound too!
- Balance each of the other elements
Now just the oxygen is out of wack, let’s fix that by adding a coefficient of two to the molecular oxygen in the reactants:
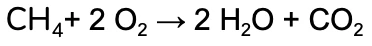
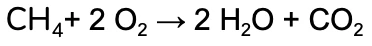
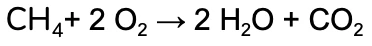



Nice! We now have the same number of each element on both the product and reactants side.
Notice that we left the oxygen (which exists on its own as O2) to last, so that we could manipulate it without affecting the number of any other element present! It’s generally a good idea to leave anything in its elemental form til last.
- Double Check!
Before you write out the final reaction, it’s always a good idea to recount the elements in your reaction, since it’s easy to lose track of elements and coefficients, especially when there are lots of compounds involved.
Ours adds up, so the final balanced chemical equation is:
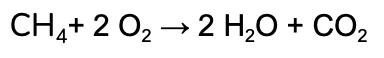
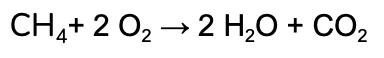
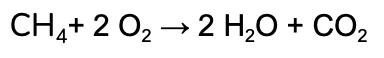
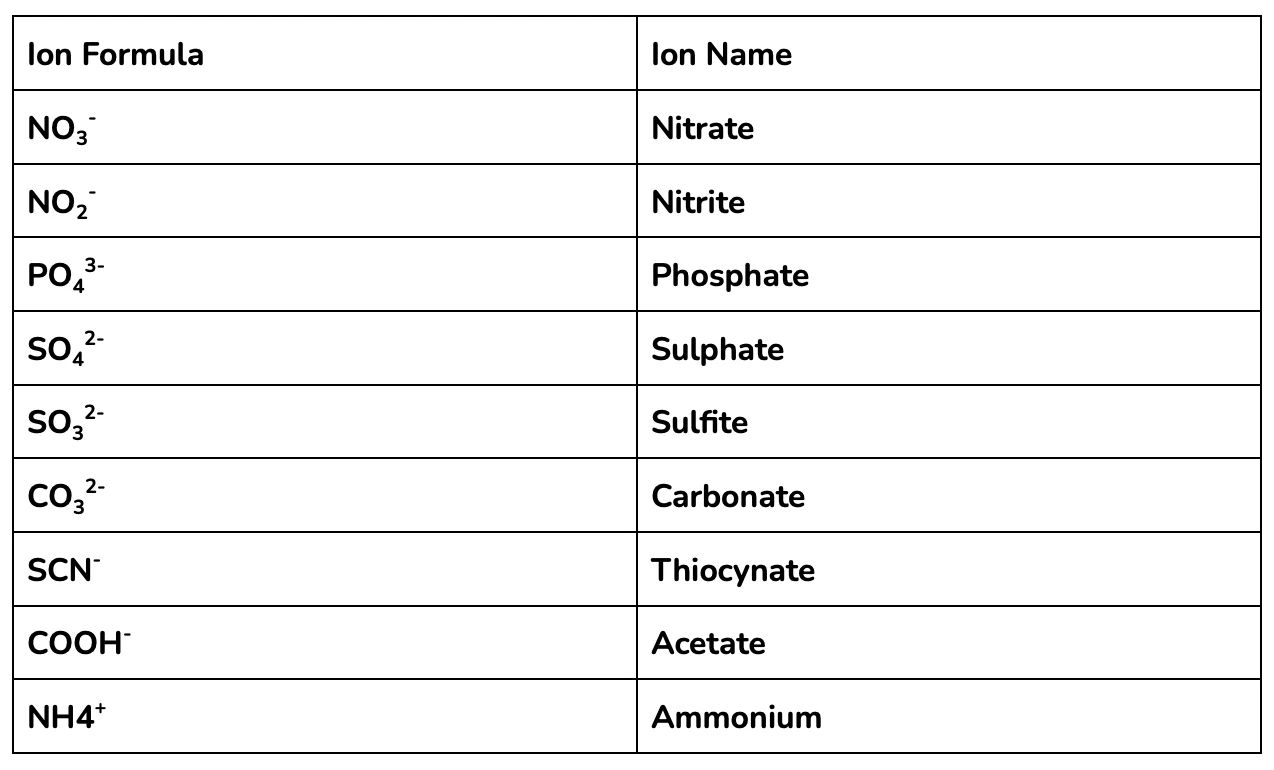
Sometimes questions will ask about compounds that include ‘polyatomic ions’, these are molecules that react as a unit, and can be kept together throughout the calculation process!
A ‘polyatomic ion’ is a charged molecule made up of multiple atoms. Polyatomic ions are central to many chemical reactions, since they are so common in the natural and industrial environments.
You should be familiar with the polyatomic ions in the table below to nail year 11 and HSC Chemistry!


If you’re interested in Chemistry, visit Project Academy’s website to get access to notes and sign up for classes!
The Chemical Mole
Now that we know that chemicals will always react in simple, whole number ratios - we need a way to determine exactly how many molecules are within that reaction! As you can imagine atoms are super tiny, so the number reacting in any observable reaction is enormous. To deal with such big numbers, we use a conversion factor so that our calculations involve simpler numbers than the sextillion (and some) that would otherwise be required.
That conversion factor is Avogadro’s Number (NA) = 6.022 x 10^23
But how big is that number really?
- If you started with $NA, and spent $1 billion every second, it would take you 19 million years to spend it all.
- Avogadro’s number grains of salt would cover the entire surface of the earth in a layer almost 17 cm thick.
That number may seem too large to be useful, but NA molecules of water make up just 18 mL! By considering Avogadro’s number we can simplify our calculations, making very large numbers much easier to manipulate.
When we have Avogadro’s Number of particles we say that we have 1 mole of particles.
6.022 x 10^23 particles = 1 mole
From this point on, instead of considering the 6.022 x 10^23 particles in the 18 mL of water, we can think about it as 1 mole.
1 chemical mole is defined as the number of carbon atoms in 12 grams of Carbon-12, which has been found to be Avogadro’s number of (or 6.022 x 10^23) atoms.
A mole is very simply a quantity of a thing. We use “quantities of things” all the time in everyday life, for example:
- Eggs are often sold by the dozen - a dozen refers to a quantity of 12
- An event may have occurred a decade ago - a decade refers to a quantity of 10
In exactly the same way, we talk about 1 mole of particles, referring to a quantity 6.022 x 10^23 particles.
This means that we can very easily convert between a number of particles and the number of moles:
- In 2 dozen eggs there are 2 x 12 eggs = 24 eggs.
- In 5.5 decades there are 5.5 x 10 decades = 55 decades
- In 3 moles of an atom there are 3 x 6.022 x 10^23 atoms = 18481 x 10^23 atoms
See now how much easier it will be to do calculations with 3 moles, compared to 18481 x 10^23 atoms!
So, to convert between moles and number of particles we use the formula:
Number of Particles = n x NA
or rearranged,
n = Number of Particles / NA
Just like the definition of the mole is based on a mass of carbon-12, we know the Molar Mass (or mass per mole) of all the stable elements - these are the mass numbers on your periodic table! If we know the mass in one mole (which we can read off the periodic table) of the substance, we can then calculate the mass of any amount of the substance using the formula:
m = MM x n
Or if we measure the mass, we can calculate the number of moles:
n = m / MM
Check out Q5 for some more practice converting between particles, mass and moles!
Concentration and Molarity
Often in chemistry we work with solutions, which is simply a liquid with something dissolved in it.
The liquid that makes up the bulk of the solution is known as the solvent. The thing that is dissolved is the solute. When you make a milo, the milk is your solvent and the milo is the solute (but the milo itself isn’t very soluble, leaving you with nice crunchy bits on top!)
We quantify the amount of solute in a solvent using concentration.
The concentration is very simply the measure of how much of one thing is dissolved in another, which we quantify using:
c = n / v
where c is the concentration and v is the volume.
Gas Laws
Lots of chemical reactions actually occur in the gaseous state, since reactions happen most quickly at high temperatures and many compounds turn into gases at high temperatures.
This means its important for us to consider the relationship between the different properties of gases:
- Number of moles (n) = the amount of gas that there is
- Volume (V) = the amount of space that gas is in
- Pressure (P) = the amount of force exerted by the gas
- Temperature (T)
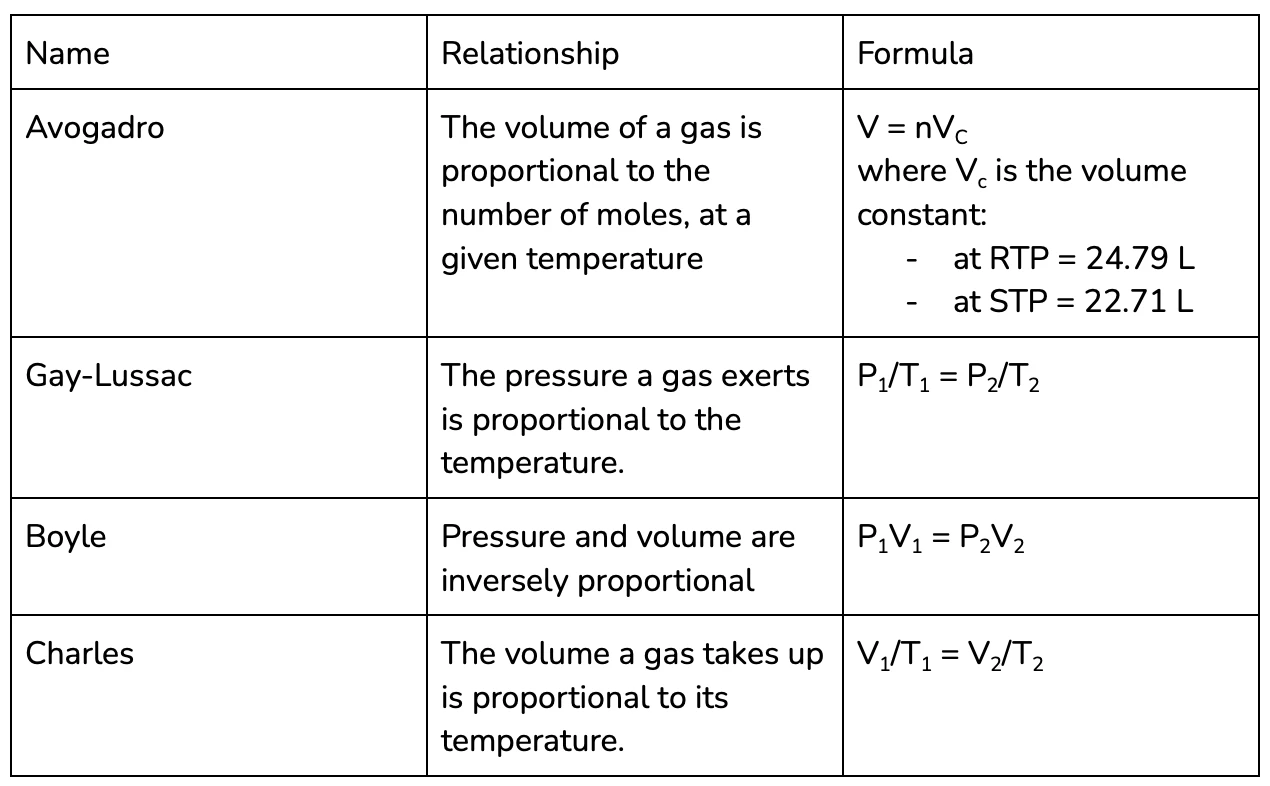


If you’re talking about a gas system at a single point, rather than comparing it at two points in time, its normally easier to use the ideal gas law.
The ideal gas law relates all of the variables associated with a gas, by the gas constant (R - on your formula sheet). Given any three variables you can calculate the value of third, using the formula:
PV = nRT
For year 11 chemistry, you do need to know the names of each of these laws as well as be able to apply them in calculations, this table is a pretty nice way to memorise them!
See Q6 for some practise using the gas laws!
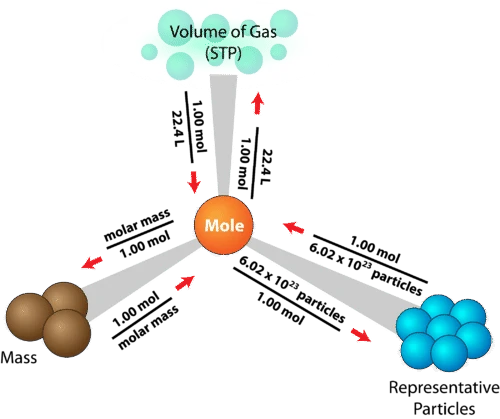
Bringing it all together
Fundamentally, Module 2 is all about converting between moles and other quantities, so that we can quantify the reactions we observe. These conversions can be summarised in a diagram like this one:


Key Experiments in Module 2 Introduction to Quantitative Chemistry
2.2.1.1. Conduct a practical investigation to demonstrate and calculate the molar mass (mass of one mole) of an element.
This experiment brings together many of the key concepts of module 2. We use the stoichiometric ratio of a known reaction to determine the number of moles of gas released by a reaction. We use that number of moles to determine the molar mass of the compound by further converting between mass and moles.
Aim: To determine the Molar Mass of Magnesium
Method:
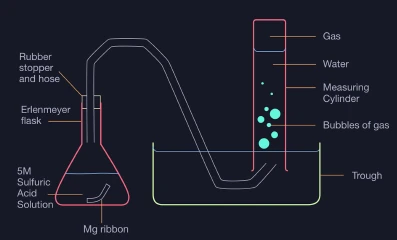


Figure 1: Experimental Apparatus
- Record the temperature and pressure of the laboratory.
- Add 30 mL of 5M sulfuric acid into an erlenmeyer flask.
- Weigh the magnesium ribbon.
- Fill a trough three quarters full with water and a measuring cylinder completely with water.
- Invert and submerge the measuring cylinder in the trough.
- Place the magnesium strip into the sulfuric acid solution and quickly put a rubber stopper with a hose over the flask with the hose being directed into the measuring cylinder.
- Observe the displacement of water from the gas.
- Record the volume of water displaced by the gas.
- Using the gas laws and mass-moles relationship, determine the molar mass of magnesium.
Example Results:



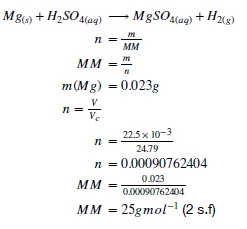
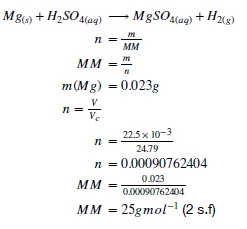
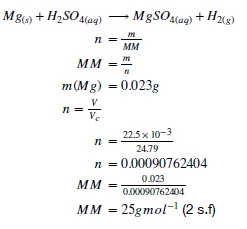
Now, this isn’t the exact molar mass of magnesium that is recorded on the periodic table - can you think of any reasons why?
2.3.1 Conduct practical investigations to determine the concentrations of solutions and investigate the different ways in which concentrations are measured
One of the key ways that the concentration of solutions is explored is through titration - a process that you’ll explore in significant detail in year 12. In order to conduct a titration, a primary standard is needed. A primary standard is a solution that is created with a precisely known concentration, through careful measuring and washing procedures.
Aim: To produce a 1.0 M Na2CO3 primary standard.
Method:
- Place an 50 g of sodium carbonate solid into a clean, dry watch glass and place in an
- oven at 105°C for 2 hours.
- Allow sodium carbonate to cool in a desiccator.
- Weigh out 26.5g of sodium carbonate into a clean, dry 50 mL beaker using an electronic balance. Record the precise mass.
- Dissolve the sodium carbonate in 30 mL of deionised water using a stirring rod and use a clean dry funnel to transfer the solution into a clean, dry 250.00 mL volumetric flask.
- Rinse the beaker and stirring rod with deionised water into the funnel ensuring all rinsing water enters the volumetric flask. Repeat this step 3 times.
- Rinse the funnel with a squirt bottle with deionised water ensuring all water enters the volumetric flask. Repeat 3 times.
- Fill the volumetric flask with deionised water until the water level is approximately 1 cm below the graduated marking.
- Add deionised water dropwise using a clean, dry dropper until the bottom of the meniscus lies on the engraved marking.
- Stopper and invert the volumetric flask 10 times.
- Calculate the precise concentration of the solution, using the measured mass.
Sample Question Bank for Module 2: Introduction to Quantitative Chemistry, Multiple Choice and Short Answer
Question 1
Samantha is preparing for a party. She’s about to begin blowing up balloons, but wants to make sure that they won’t pop as they heat up throughout the day.
Which gas law might she use to investigate the effect of temperature on the pressure inside the balloon?
- Gay Lussac’s Law
- Avogadro
- Boyle
- Charles
Question 2
Harry has been asked to identify the limiting reagent of a chemical reaction. He should look for:
- Any products that are formed
- The reactants that are initially in the vessel
- The first reactant that is used up completely
- The product that forms last
Question 3
Belinda is working really hard to practise balancing chemical equations, because she knows it’s crucial for success in year 11 Chemistry. Which equation has Belinda balanced correctly?
- C8H18 + 25O2⟶ 8CO2+ 9H2O
- 6CO2 + 6H2O → C6H12O6 + 6O2
- C6H12O6 + 4O2 → 6CO2 + 3H2O
- 4CO + 2O2 → 2CO2
Bonus Question - have a go balancing the other equations yourself :)
Question 4
Calculate the following:
(A) The volume of steam formed in the reaction of 3.6 L of Hydrogen gas and excess Oxygen gas - 2 Marks.
2H2(g) + O2(g)⟶2H2O(g)
Ratio is 2:1:2 therefore there are equal amounts of hydrogen and water in excess oxygen.
∴ There is 3.6 L of steam.
(B) The volume of Nitrogen gas and Hydrogen gas required to form 6.0 L of Ammonia - 2 Marks.
N2(g) + 3H2(g)⟶2NH3(g)
Ratio is 1:3:2.
∴ If 6 L of ammonia are formed, 9 L of hydrogen was required and 3 L of nitrogen.
(C) The volume of Nitrogen Dioxide gas formed from the reaction between 2.0 L of Nitrogen and 3.8 L of Oxygen - 2 Marks.
N2(g) + 2O2(g)⟶2NO2(g)
Ratio is 1:2:2.
For 2 L of nitrogen to fully react, 4 L of oxygen is required.
For 3.8 L of oxygen to fully react, 1.9 L of nitrogen is required.
∴ Oxygen is the limiting reagent (as there is not enough oxygen to react all the nitrogen) and hence will react completely.
As the amount of oxygen = amount of nitrogen dioxide due to the ratio, 3.8 L of nitrogen dioxide is formed.
Question 5
Sarah is making her evening chocolate milk and has decided to apply her new chemistry knowledge to her treat.
(A) If she mixes 10 g of chocolate powder into 100 mL of milk, what is the concentration of the chocolate milk in g/L?
Step 1:
Always check your units first. They’ve asked for the answer in grams per litre, so we should convert the volume measurement to litres.
100 mL = 0.1 L
Step 2:
Concentration = amount of solute / amount of solvent
= amount of chocolate powder / amount of milk
= 10 g / 0.1 L
= 100 g / L
(B) If the chocolate powder has a molar mass of 180 g/mol, what is the molar concentration of the chocolate milk?
Step 1:
Converting between mass and moles using n = m / MM
N = 10 g / 180 g/mol
= 0.0555… moles
Step 2:
Calculating concentration using c = n/v
c = 0.0555… moles / 0.1 L
= 0.55 M
(C) How many particles of chocolate milk did Sarah use?
Calculating using number of particles = n x NA
= 0.0555… x 6.022 x 10^23
= 3.345 x 10^22 particles
Question 6
A hot air balloon works on the principle that the gas inside will expand as it rises and the surrounding pressure decreases. Assume that there are 10 moles of Helium gas in the balloon, and it can expand to hold 12 000 L.
(A) At RTP, what volume will the balloon take up? - 2 Marks.
Using the ideal gas law Avogadro’s Law:
V = nVc
= 10 x 24.79
= 247.9 L
Note: you could also use the ideal gas law, but this is simpler.
(B) Assuming that it stays on the ground, what change in temperature would be required to double the volume of the balloon? - 2 Marks.
Using Charles’ Law:
V1/T1 = V2/T2
T2 = V1/T1V2
= 247.9 / (25 x 495.8)
= 0.02 C
Change = 25 - 0.02
= 24.98 C
(C) Assuming that the temperature in the sky is -10 C, at what pressure will the hot air balloon completely fill with gas? -2 Marks.
Using the ideal gas law:
PV = nRT
P = nRT / V
= 10 x 8.134 x 263 / 12 000
= 1.78 Pa (that’s about 1 / 100th of the pressure at Earth’s surface, I hope they took oxygen masks!)
If you want more practice questions and papers, why not trial our year 11 Chemistry courses?







